จอร์จ บูล (George Boole) คือใคร? พร้อมประวัติและผลงานของจอร์จ บูล

จอร์จ บูล (George Boole) หลายคนอาจจะไม่รู้จักว่าเขาเป็นใคร แต่ถ้าคนที่อาจจะรู้จักเขาในฐานะผู้ค้นคิด “พีชคณิตแบบบูล” วันนี้ Zcooby ขอแนะนำข้อมูลที่น่าสนใจไม่ว่าจะเป็นประวัติและผลงาน รวมทั้งข้อมูลเกี่ยวกับ พีชคณิตแบบบูล มาฝากกันนะครับ

จอร์จ บูล (George Boole) คือใคร?

เขาเป็นนักคณิตศาสตร์และนักปรัชญาชาวอังกฤษ มีผลงานสำคัญคือ การค้นคิด พีชคณิตแบบบูล (Boolean algebra) ซึงได้กลายมาเป็นรากฐานสำคัญของตรรกศาสตร์ และ วงจรดิจิตอล โดยวันที่ 2 พฤศจิกายน 2558 เป็นวันครบรอบวันเกิด 200 ปี ของจอร์จ บูลครับ

George Boole

ประวัติของ จอร์จ บูล (George Boole)

เขาเกิดเมื่อวันที่ 2 พฤศจิกายน ปี 1815 ที่เมืองลินคอร์น ประเทศอังกฤษ บิดาชื่อ จอห์น บูล (1779-1848) เขาได้ศึกษาในคณิตศาสตร์ชั้นสูง และได้ทำงานเป็นครูสอนคณิตศาสตร์อยู่ตามโรงเรียนเป็นช่วงสั้นๆ

จนกระทั่ง ในปี 1849 เขาได้เป็นศาสตราจารย์ทางคณิตศาสตร์ที่ Queen’s College Cork (ปัจจุบันเปลี่ยนชื่อเป็น University College Cork อยู่ในประเทศไอร์แลนด์) ในที่นี้เขาได้ศึกษาและตีพิมพ์วรสารทางวิชาการหลายงาน ซึ่งมักจะเกี่ยวกับ สมการเชิงอนุพันธ์ และแคลคูลัส

ในปี 1854 เขาได้ตั้งข้อสังเกตในความคล้ายคลึงกันระหว่างระบบบวก คูณ และระบบตรรกศาสตร์และ หรือ จึงสร้างระบบพีชคณิตแบบบูล (พีชคณิตแบบบูลนำเทคนิคทางพีชคณิตมาใช้กับนิพจน์ในตรรกศาสตร์เชิงประพจน์) ในงานของเขาที่ชื่อว่า An Investigation of the Laws of Thought, on Which are Founded the Mathematical Theories of Logic and Probabilities (มักเรียกสั้นๆว่า The Law of thought) ซึ่งยังไม่มีชื่อเสียงในขณะนั้น

ในปี 1855 เขาได้แต่งงานกับ แมรี่ เอเวอร์เรสต์ (ซึ่งลุงของเธอ จอร์จ เอเวอร์เรสต์ เป็นนักสำรวจในอินเดียที่มีชื่อเสียง และยอดเขาเอเวอร์เรสต์ก็ตั้งมาจากนามสกุลนี้นั้นเอง) ซึ่งเธอมีบทบาทในการช่วยทำงานของสามีเธอเป็นอย่างยิ่ง ระหว่างนั้นจอร์จ บูลก็ยังคงศึกษาทางตรรกะ และคณิตศาสตร์เรื่อยมา (ในสมัยนั้นยังไม่รวมเป็นวิชาเดียวกัน)

จอร์จ บูลเสียชีวิตด้วยโรคติดเชื้อในปอดเมื่อวันที่ 8 ธันวาคม ปี 1864 ที่ Ballintemple, Cork ประเทศไอร์แลนด์ รวมอายุ 49 ปี หลังจากที่เขาเสียชีวิตไป 73 ปีแล้ว ผลงาน พีชคณิตแบบบูล นั้นได้กลับมาได้รับความสนใจอีกครั้งโดยคลาวด์ อี. แชนนอน นักวิทยาศาสตร์แห่งห้องทดลองเบลล์ (Bell Laboratory) ได้นำพีชคณิตแบบบูลมาประยุกต์ใช้ในการออกแบบวงจรดิจิตอลและใช้กันอยู่จนถึงปัจจุบัน

ผลงานของจอร์จ บูล (George Boole)

ผลงานที่สำคัญของจอร์จบูลก็คือ พีชคณิตแบบบูล (Boolean algebra) โดยชื่อพีชคณิตแบบบูลนั้นตั้งตามจอร์จ บูล ผู้พัฒนาพีชคณิตแบบนี้

พีชคณิตแบบบูล คืออะไร

พีชคณิตแบบบูล (Boolean algebra) (หรือ พีชคณิตบูลีน หรือ แลตทิซแบบบูล)คือโครงสร้างเชิงพีชคณิตซึ่งเป็นการรวบรวมแก่นความหมายของการดำเนินการทางตรรกศาสตร์และทฤษฎีเซต

รูปแบบของพีชคณิตแบบบูล

พีชคณิตแบบบูล คือ เซต A ที่ประกอบด้วยการดำเนินการทวิภาค คือ $\land$ (AND) กับ $\lor$ (OR) , การดำเนินการเอกภาค คือ $\lnot$ / ~ (NOT) และสมาชิกคือ 0 (FALSE) กับ 1 (TRUE) ซึ่งสำหรับสมาชิก a, b และ c ของเซต A จะมีคุณสมบัติเป็นไปตามสัจพจน์เหล่านี้

สมบัติของ $\lor$	สมบัติของ $\and$	ชื่อเรียก
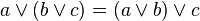$a \lor (b \lor c) = (a \lor b) \lor c$	$a \land (b \land c) = (a \land b) \land c$	การเปลี่ยนหมู่
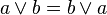$a \lor b = b \lor a$	$a \land b = b \land a$	การสลับที่
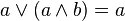$a \lor (a \land b) = a$	$a \land (a \lor b) = a$	absorption
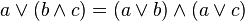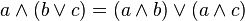$a \lor (b \land c) = (a \lor b) \land (a \lor c)$	$a \land (b \lor c) = (a \land b) \lor (a \land c)$	การแจกแจง
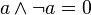$a \lor \lnot a = 1$	$a \land \lnot a = 0$	ส่วนเติมเต็ม

สำหรับสมาชิก a และ b ใน A มันจะมีเอกลักษณ์ดังต่อไปนี้

สมบัติของ $\lor$	สมบัติของ $\and$	ชื่อเรียก
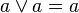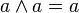$a \lor a = a$	$a \land a = a$	นิจพล (idempotency)
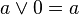$a \lor 0 = a$	$a \land 1 = a$	มีขอบเขต (boundedness)
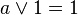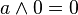$a \lor 1 = 1$	$a \land 0 = 0$	มีขอบเขต (boundedness)
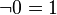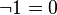$\lnot 0 = 1$	$\lnot 1 = 0$	0 และ 1 เป็นส่วนเติมเต็มกัน
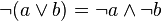$\lnot (a \lor b) = \lnot a \land \lnot b$	$\lnot (a \land b) = \lnot a \lor \lnot b$	กฎเดอมอร์แกน (de Morgan’s laws)
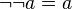$\lnot \lnot a = a$		อวัตนาการ (involution)

ตัวดำเนินการของบูล

ตรรกศาสตร์	ทฤษฏีเซต	วงจรดิจิตอล
$true$	$U$ (เอกภพสัมพัทธ์)	$1$
$false$	$\emptyset$ (เซตว่าง)	$0$
$\lor$	$\cup$	$+$
$\land$	$\cap$	$\cdot$

การนำไปใช้

เรานำพีชคณิตแบบบูลไปใช้ในตรรกศาสตร์ได้ โดยตีความให้ 0 หมายถึง เท็จ, 1 หมายถึง จริง, ∧ แทนคำว่า และ, ∨ แทนคำว่า หรือ, และ ¬ แทนคำว่าไม่
พีชคณิตแบบบูลที่มีสมาชิก 2 ตัวนั้น นำไปใช้ประโยชน์ในการออกแบบวงจรไฟฟ้าในงานวิศวกรรมไฟฟ้าได้ โดย 0 และ 1 แทนสถานะที่แตกต่างกันของบิตในวงจรดิจิทัล นั่นก็คือสถานะศักย์ไฟฟ้าสูงและต่ำ

จอร์จ บูล (George Boole) คือใคร? พร้อมประวัติและผลงานของจอร์จ บูล